$\newcommand{\d}{\mathrm{d}} \newcommand{\bff}{\boldsymbol{f}} \newcommand{\bfg}{\boldsymbol{g}} \newcommand{\bfp}{\boldsymbol{p}} \newcommand{\bfq}{\boldsymbol{q}} \newcommand{\bfx}{\boldsymbol{x}} \newcommand{\bfu}{\boldsymbol{u}} \newcommand{\bfv}{\boldsymbol{v}} \newcommand{\bfA}{\boldsymbol{A}} \newcommand{\bfB}{\boldsymbol{B}} \newcommand{\bfC}{\boldsymbol{C}} \newcommand{\bfM}{\boldsymbol{M}} \newcommand{\bfJ}{\boldsymbol{J}} \newcommand{\bfR}{\boldsymbol{R}} \newcommand{\bfT}{\boldsymbol{T}} \newcommand{\bfomega}{\boldsymbol{\omega}} \newcommand{\bftau}{\boldsymbol{\tau}}$

Principles of force control

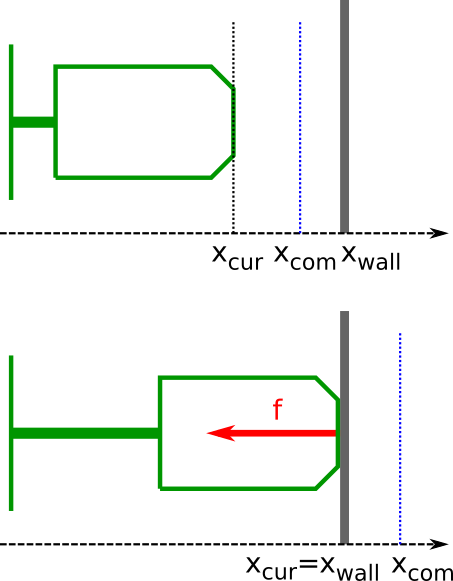
Consider a 1-DOF, linear, position-controlled robot as in the figure below. One would like to control the contact force $f$ between the robot end-effector and the wall so as to track a reference $f_\mathrm{ref}$, where $f_\mathrm{ref}$ is, for example, a constant positive value.

For that, one can use a Proportional-Derivative (PD) control law as below. Note that the command sent to the robot is $x_\mathrm{com}$ is a desired position.

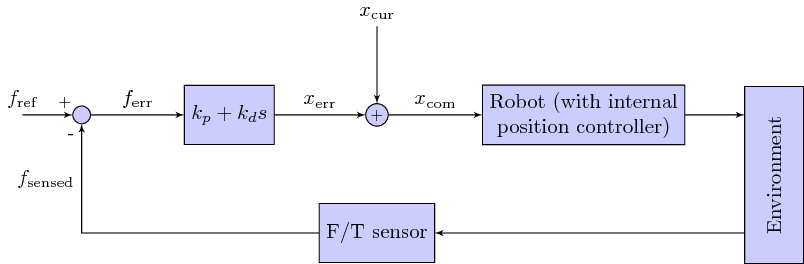
The Force/Torque (F/T) sensor measures the contact force between the end-effector and the wall. When there is no contact (first figure, top sketch), the contact force is zero, thus $f_\mathrm{sensed}=0$, yielding $f_\mathrm{err}>0$. Assuming stationary initial conditions, one has next $x_\mathrm{err}>0$, which implies that $x_\mathrm{com}>x_\mathrm{cur}$, which in turn makes the robot move to the right, towards the wall.

Upon contact between the robot end-effector and the wall (first figure, bottom sketch), the contact force sensed by the F/T sensor $f_\mathrm{sensed}$ becomes positive, but initially smaller than $f_\mathrm{ref}$ – assuming "soft" collision. Therefore, initially, one still has $x_\mathrm{com}>x_\mathrm{cur}=x_\mathrm{wall}$, meaning that the robot is commanded to penetrate the wall.

Finally, interactions between the PD controller and the stiffness of the end-effector, of the wall, and of the robot's internal position controller (characterized in part by its own PID gains), will eventually lead to a stationary state where $f_\mathrm{err}=0$ and $x_\mathrm{com}>x_\mathrm{wall}$ (so as to ensure a positive contact force).